Náhodná čísla a třída Random
Tento článek byl napsán v roce 2015. Vývojářské technologie se neustále inovují a článek již nemusí popisovat aktuální stav technologie, ideální řešení a můj současný pohled na dané téma.
Zaujaly mě některé otázky na Stack Overflow, které souvisí s tím, nakolik jsou čísla generovaná pomocí třídy Random v .NET náhodná. Protože je toto téma celkem často opírané, rozhodl jsem se k tomu napsat několik vlastních poznatků, respektive faktů.
Třída Random
Třída Random je tu s náma už od verze .NET frameworku 1.1., nicméně použitelná tak jak ji zhruba známe je od verze 2.0. Technicky se jedná o generátor pseudo-náhodných čísel. Algoritmus napsal prof. D. E. Knuth z Harvardu a je založen na principu lineárního kongruenčního generátoru. Ten tvoří náhodná čísla na základě vzorce s pomocí modulo a dalších zvolených konstant. Obecný předpis takového generátoru je:
xi+1 = axi+c (mod m)
Algoritmus D. E. Knutha používá pro konstanty různá magická čísla. Jedním z nich, které můžeme v implementaci najít je například poměrové číslo označované jako Golden Ratio, česky "Zlatý řez". Algoritmem se nemá smysl dále zabývat, jelikož je důkladně popsán v příručce The Art of Computer Programming, Volume 2: Seminumerical Algorithms
Instance třídy
Třída Random má dva konstruktory. Obvykle vývojář použije ten bezparametrický, který implicitně použije hodnotu Environment.TickCount a předá ji jako hodnotu do druhého konstruktoru Random(int seed). Environment.TickCount vrací čas v milisekundách od spuštění systému. Pokud bychom si nechali v cyklu vypsat hodnotu této property, zjistíme, že cyklus je tak rychlý, že property bude vracet na konzoli často stejná čísla. A to dokonce s použitím uspání vlákna, např.:
for (int i = 0; i < 20; i++)
{
Thread.Sleep(1);
Console.WriteLine("{0}: {1}", i, Environment.TickCount);
}
To má za následek fakt, že pokud bychom měli potřebu generovat náhodná čísla bez udání seedu pomocí dvou generátorů, jako nevhodná implementace se jeví:
Random random1 = new Random(); Random random2 = new Random();
S vysokou pravděpodobností takto vytvoříme dva generátory, které mají stejný seed. Správné řešení je použití vlastního seedu, například s pomocí Guid.
Random random = new Random(Guid.NewGuid().GetHashCode());
Seed je defacto nějaký výchozí prvek, od kterého jsou náhodná čísla deterministicky generována. Jinými slovy, pokud vytvoříme instanci třídy Random a předáme jako seed například číslo 99, vždy se bude generovat stejná číselná řada (za předpokladu stejného intervalu při opakovaném volání metody Next(int, int)).
Pro zajímavost (a z logiky věci) - pokud bychom se stejným seed generovali čísla o vyšším rozsahu ale s minimálním rozdílem horní hodnoty, získali bychom dvě velmi podobné řady náhodných čísel. Např.:
Random random1 = new Random(99);
Random random2 = new Random(99);
for (int i = 0; i < 10; i++)
{
Console.WriteLine("R1: {0}", random1.Next(1,500));
Console.WriteLine("R2: {0}", random2.Next(1,501));
Console.WriteLine();
}
Nakonec ještě poznamenám, že vložené číslo seed není konečné, právě toto číslo je dále dopočítáno s pomocí Golden Ratio.
Next(int, int)
Volání metody Next(int minValue, int maxValue) vrátí další náhodné číslo ve stanoveném rozsahu. Zajímavé je, že hodnota maxValue udává ve skutečnosti horní hranici o jednotku menší, tedy maxValue - 1.
Náhodné nebo ne?
Stále jsme se nedostali k tomu, zda jsou generované řady náhodné. Mohl bych napsat ano, stejně jako je to uvedeno v MSDN nebo v práci prof. D. E. Knutha ale pro zajímavost můžeme udělat pár testů. Aby byl test objektivní, je ideální pracovat s 1000 náhodnými čísly a vyzkoušet různé hodnoty pro seed. Tu práci jsem si již dal, proto jen demonstruji výsledky například na seed = 99 a pro interval <0;50>. Testy nebudu popisovat a opět jen odkážu na zdroje.
Kolmogorov-Smirnov test
Kritická hodnota pro test při hladině významnosti 0,05 pro 1000 prvků je 0,0430. Generovaná řada byla seskupena dle četností a testové kritérium Dn = 0,024. Protože testové kritérium nedosáhlo kritické hodnoty, nezamítáme nulovou hypotézu o shodě prvků a lze říct, že generovaná řada náhodných čísel splňuje podmínky pro statistickou náhodnost na hladině významnosti 0,05.
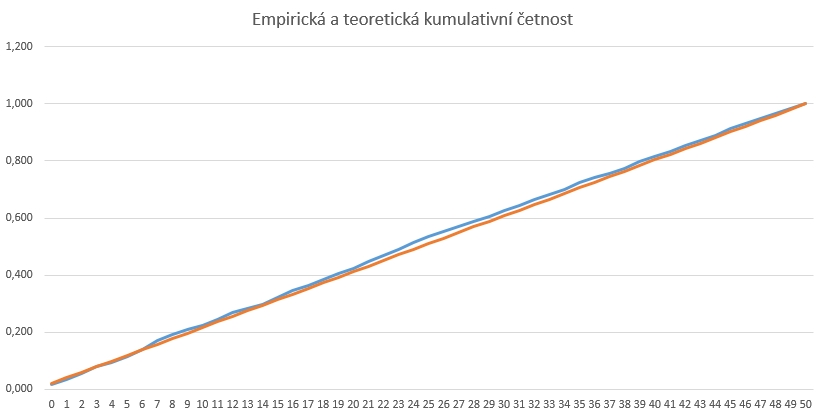
Na dalším obrázku je vidět rozložení odchylek pro všechny hodnoty v generovaném intervalu (jako absolutní číslo).
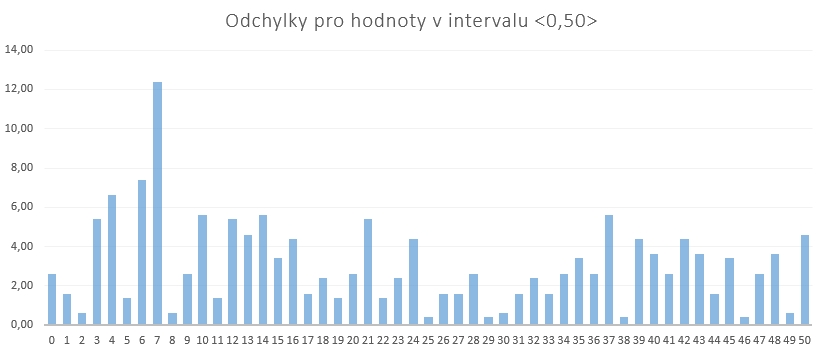
Pro zajímavost, podobně dopadly i testy pro další zvolené hodnoty pro seed.
D 0.043 seed 5 Dn 0.025 seed 99 Dn 0.024 seed 256 Dn 0.021 seed 314 Dn 0.028 seed 1024 Dn 0.017 seed 102254 Dn 0.030 seed 256345 Dn 0.028 seed 256346 Dn 0.018 seed 256347 Dn 0.018 seed 999999 Dn 0.018
Chí-kvadrát test (shoda rovnoměrného rozd.)
Opět je nalezena kritická hodnota testu pro k-1 prvků (četnosti 0-50). D = 46,214 a dopočteno je testové kritérium Dn = 37,034. Opět testové kritérium nedosáhlo kritické hodnoty a můžeme tedy učinit stejný závěr jako v předchozím případě (stejná hladina významnosti). Pro zajímavost jen výsledky pro další seed hodnoty:
D 37,034 seed 5 Dn 52,538 seed 99 Dn 37,034 seed 256 Dn 40,910 seed 314 Dn 56,720 seed 1024 Dn 44,378 seed 102254 Dn 50,192 seed 256345 Dn 48,254 seed 256346 Dn 53,558 seed 256347 Dn 48,050 seed 999999 Dn 46,214
Další testy
Vynechal jsem lokální testy, které by měly ještě potvrdit náhodnost v případě rozdělení generované řady na menší části. Udělal jsem ale nad celou řadu i testy bodů zvratu a znamének diferencí. Výsledky dopadly dle očekávání:
Test bodů zvratu n = 1000 P = 644 (počet diferencí) U = 1,96 Un = -1,6015 U > |Un| (potvrzena náhodnost) Test znamének diferencí n = 1000 C = 496 (počet bodů růstu) U = 1,96 Un = -0,38321 U > |Un| (potvrzena náhodnost)
Pár hodů kostkou
Nakonec jsem se rozhodl ještě vyzkoušet, jak třída Random obstojí pro simulaci hodu kostkou. Kdybychom měli teoreticky 100% vyváženou kostku a učinili bychom dostatečné množství pokusů (konečné číslo blízké ∞), prakticky by počet hodů každého čísla měl být velmi blízko teoretické hodnotě pravděpodobnosti. Pravděpodobnost, že padne jakékoliv číslo na kostce v rámci jednoho hodu je samozřejmě 1/6 (cca 0,166666...).
Generované rozsahy čísel odpovídaly předpokladu. Diference minimální a maximální hodnoty se pohybovala mezi 0,022 a 0,028 pro různě zvolené seed. Průměrná odchylka od očekávané hodnoty byla v rozmezí 0,0052222 a 0,010889. To všechno při 1000 iteracích (náhodných pokusech).
Následně jsem test provedl na 1 milionu iterací se zajímavými výsledky. Diference min a max hodnoty byla menší než 0,0014 a průměrná odchylka se od očekávané hodnoty zmenšila na cca 0,00024 až 0,00039 pro různé seed hodnoty. Se zvyšováním počtu iterací se tedy průměrná odychylka zmenšuje. Na obrázku níže můžete vidět závislost lineárně se zvyšujícího počtu iterací a chování průměrné odchylky pro počet iterací od 1000 do 1 mil.
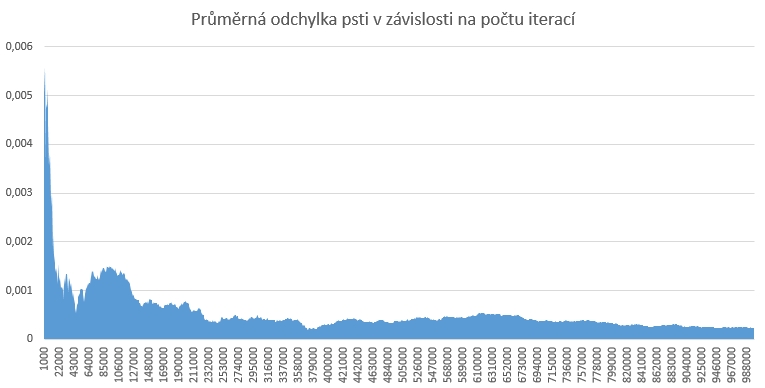
Když vybereme větší kroky v počtu iterací, je zpřesnění zřejmé:
iterations avg d. 10 0,116666667 100 0,015 1000 0,005055556 10000 0,002883333 100000 0,001390556 1000000 0,000240611 10000000 8,18E-05 100000000 2,34E-05
Závěry a shrnutí
V článku jsem nastínil jakým způsobem funguje třída Random. Splňuje základní předpoklady statistické náhodnosti, což jsme pro zajímavost otestovali několika testy na zvolené hladině významnosti. Pokud chceme třídu Random použít, je potřeba hlídat si horní hodnotu v metodě Next(int, int), která ve skutečnosti odpovídá max-1 (což je jeden z mála code smell ve třídě). Pro generování náhodných řad doporučuji používat vlastní seed, buď vytvořený náhodně pomocí hashe z Guid.NewGuid() nebo s vlastní hodnotou.
